Assessing the new class of d-i-d estimators

A replication

Dan Killian

DALL-E interpretation of my final preparation

Outline of presentation

  • Background
  • Problem
  • Solutions
  • Case study - MISTI
  • Final thoughts

Bottom line up front

  • In certain settings, beware the Two-Way Fixed Effects Estimator!
  • Don’t conflate your modeling approach (TWFE) with your estimation strategy
  • Examine the different groups created by differential timing
  • Use event study designs
  • Specify a fully flexible model (Two-way Mundlak)
  • Background
  • Problem
  • Solutions
  • Case study - MISTI
  • Final thoughts

D-i-D has a long and storied history

  • Ignaz Semmelweis - Let’s track mortality rates in two maternity wards, one staffed with midwives and the other with medical students (who were busy with cadavers)

D-i-D has a long and storied history

  • John Snow: Let’s track cholera infection in two London neighborhoods, one with treated water and one without

John Snow

Jon Snow

D-i-D has a long and storied history

  • Economists - Let’s steal repeated measures ANOVA from the statisticians!

  • “This estimator has been labeled the difference-in-differences estimator in the recent program evaluation literature, although it has a long history in analysis of variance.” [Wooldridge 2010]

  • Cross Validated: Difference in Difference vs repeated measures

So what is the canonical d-i-d setup?

\(y_{it}=\beta_0+\delta_{0,t}Post_t+\beta_{1,i}Treat_i+\delta_{1,it}Post_t*Treat_i+\epsilon_{it}\)

where..

\(\beta_0\) is the comparison group at baseline

\(\delta_0\) is the secular change from baseline to endline, unrelated to treatment

\(\beta_1\) is the difference between the treatment and comparison groups at baseline, and

\(\delta_1\) is the treatment effect, the interaction of treatment and time

Algebraically, \(\delta_0\) can be expressed as the difference between the pre/post difference in each of the treatment and comparison groups

\(\delta_1=\)

\((\bar{y}_{POST,TREAT}-\bar{y}_{PRE,TREAT})\)

\(-\)

\((\bar{y}_{POST,COMPARISON}-\bar{y}_{PRE,COMPARISON})\)

hence, difference-in-differences (d-i-d or DiD or DD)

Canonical d-i-d, 2x2

\(y_{it}=\beta_0+\delta_{0,t}Post_t+\beta_{1,i}Treat_i+\delta_{1,it}Post_t*Treat_i+\epsilon_{it}\)

Canonical d-i-d 2x2 setup
Pre Post Post - Pre
Comparison \(\beta_0\) \(\beta_0+\delta_0\) \(\delta_0\)
Treatment \(\beta_0+\beta_1\) \(\beta_0+\delta_0+\beta_1+\delta_1\) \(\delta_0+\delta_1\)
Treatment - Comparison \(\beta_1\) \(\beta_1 + \delta_1\) \(\delta_1\)

How does the canonical d-i-d generalize to multiple time periods and/or groups?

When we generalize the two-period setup to multiple time periods and/or groups, we have the two-way fixed effect (TWFE) estimator

\(y_{it}=\alpha_i+\alpha_t+\beta^{DD}{it}+\epsilon_{it}\)

where..

\(\alpha_i\) are group fixed effects

\(\alpha_t\) are time fixed effects

\(B^{DD}_{it}\) indicates whether group i in period t is treated

TWFE is a workhorse in program evaluation

  • 744 d-i-d studies across ten journals in finance and accounting, 2000-2019 [Baker 2022]

  • 19 percent of all empirical articles published by the American Economic Review (AER) between 2010 and 2012 used TWFE [de Chaisemartin and D’Haultfoeuille 2020]

  • Background
  • Problem
  • Solutions
  • Case study - MISTI
  • Final thoughts

But what is \(\beta^{DD}_{it}\) actually telling us?

  • For the canonical 2x2, we know exactly what we are estimating

  • For i groups and t time periods, we are getting some average of multiple 2x2s

  • But how does this work, exactly?

  • Goodman-Bacon (2021) decided to work it out

Let’s take a single step from two time periods to three, where treatment can be adopted at either t = 2 or t = 3

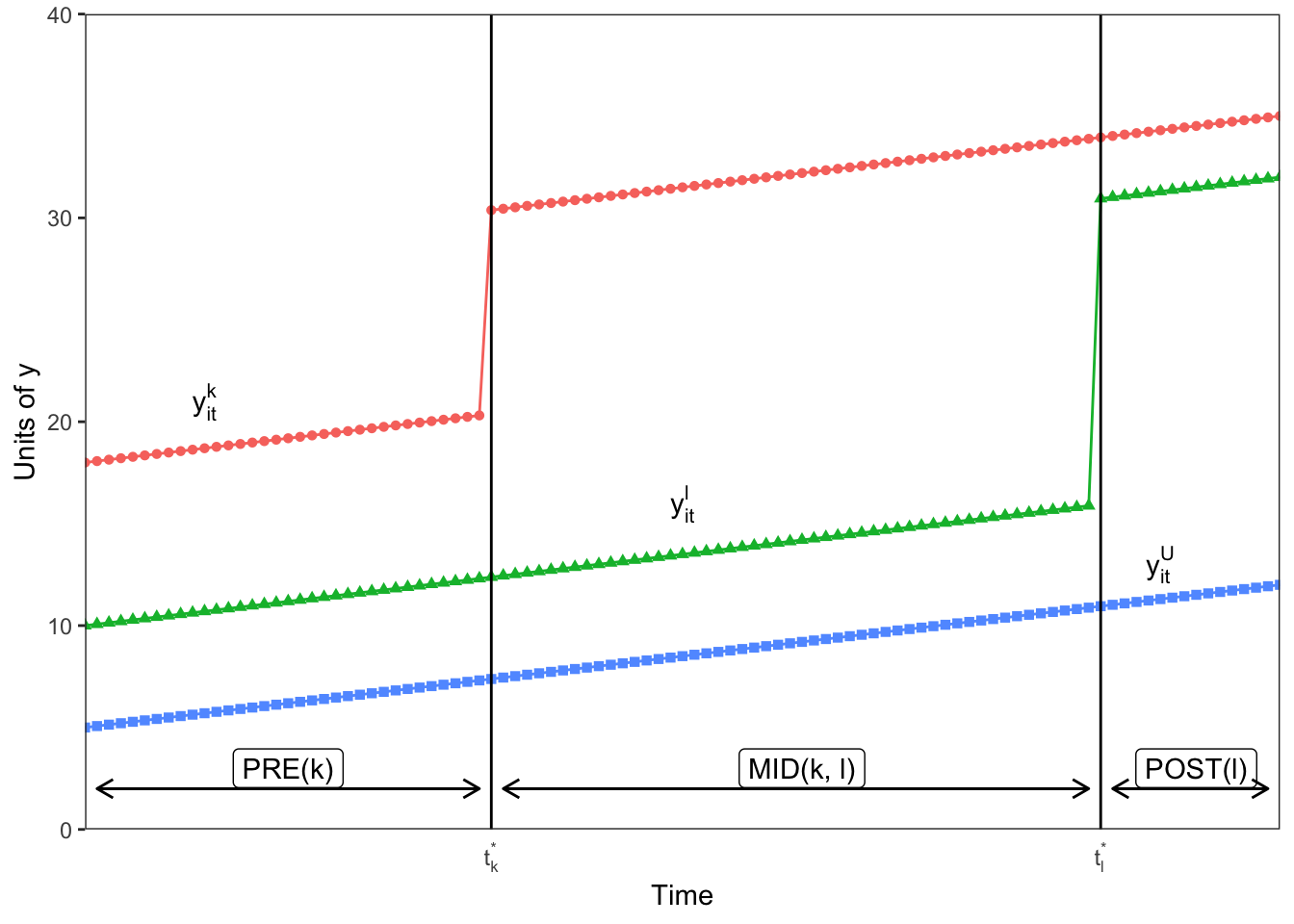
Any design with multiple treatment timings will have \(k^2\) groups, where k is the number of timings.

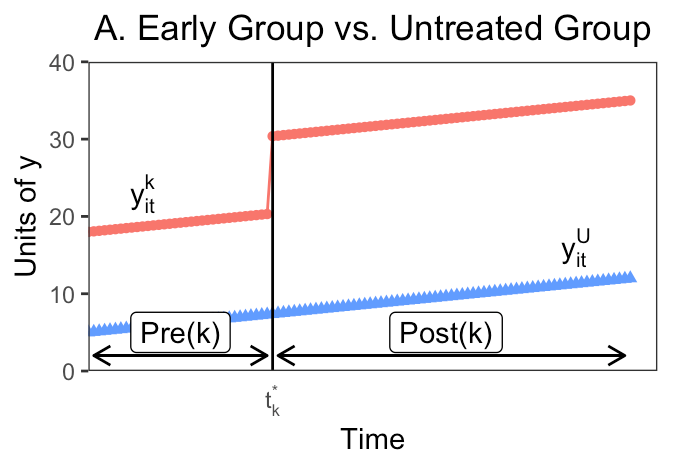
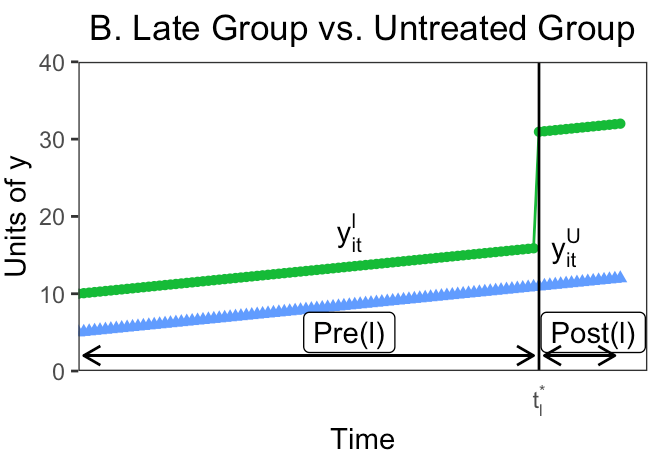
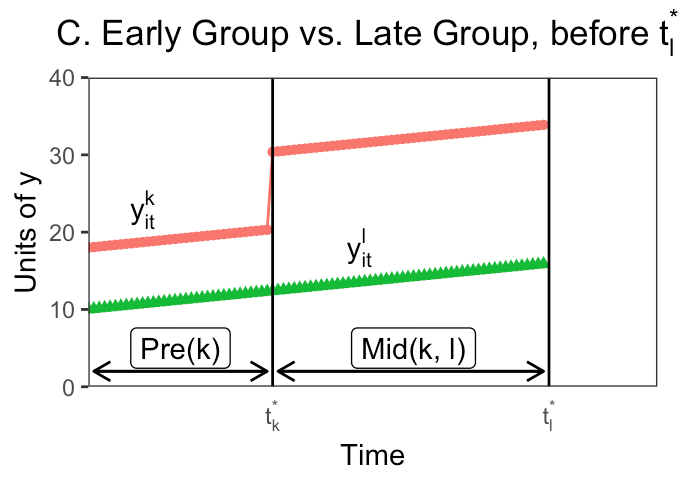
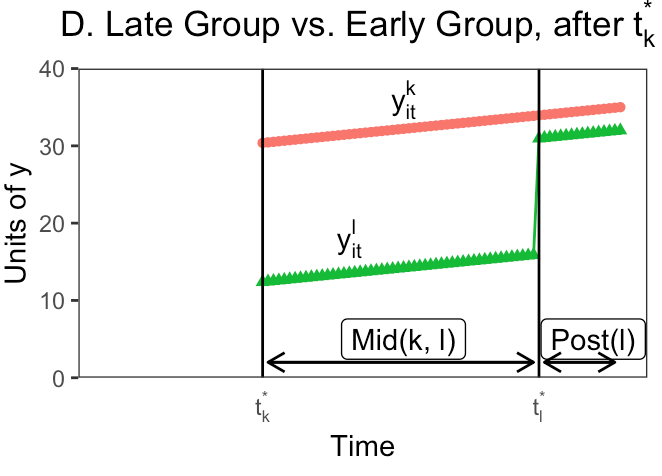
Where does this leave us?

  • TWFE treats some data that is under treatment status as comparison!
  • Not an issue under constant treatment effect
    • stable unit treatment value (SUTVA)
    • no variation in treatment effect for any reason

But TWFE fails under following conditions:

  • different treatment groups have different treatment effects
  • treatment effects are dynamic over post-treatment periods
  • heterogeneous treatment effects across sub-groups within a treated group

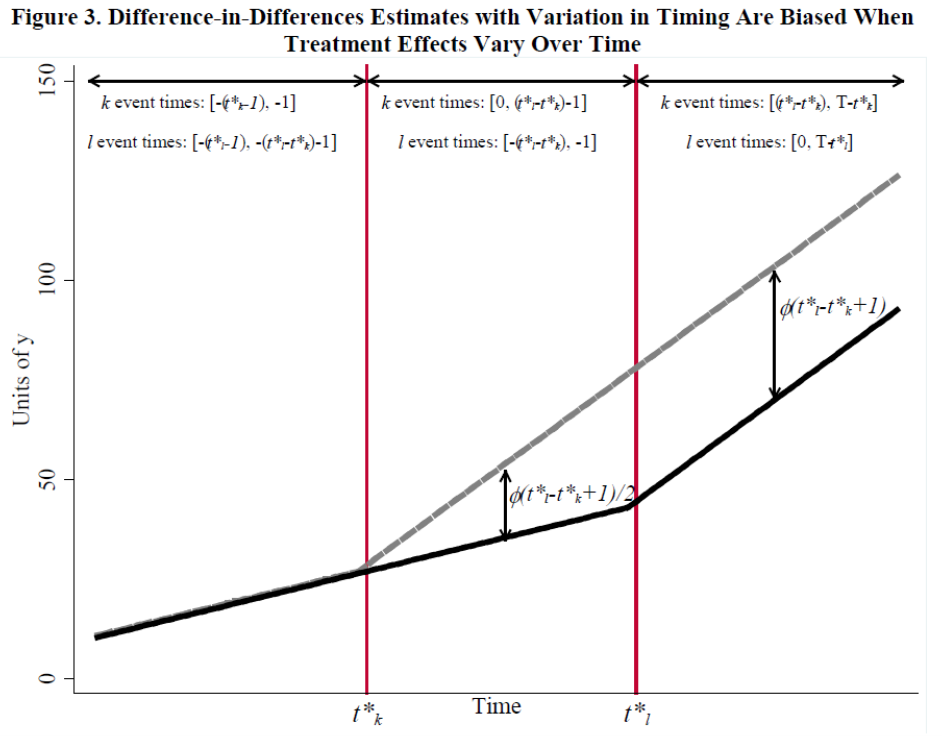
An example of failure

  • Background
  • Problem
  • Solutions
  • Case study - MISTI
  • Final thoughts

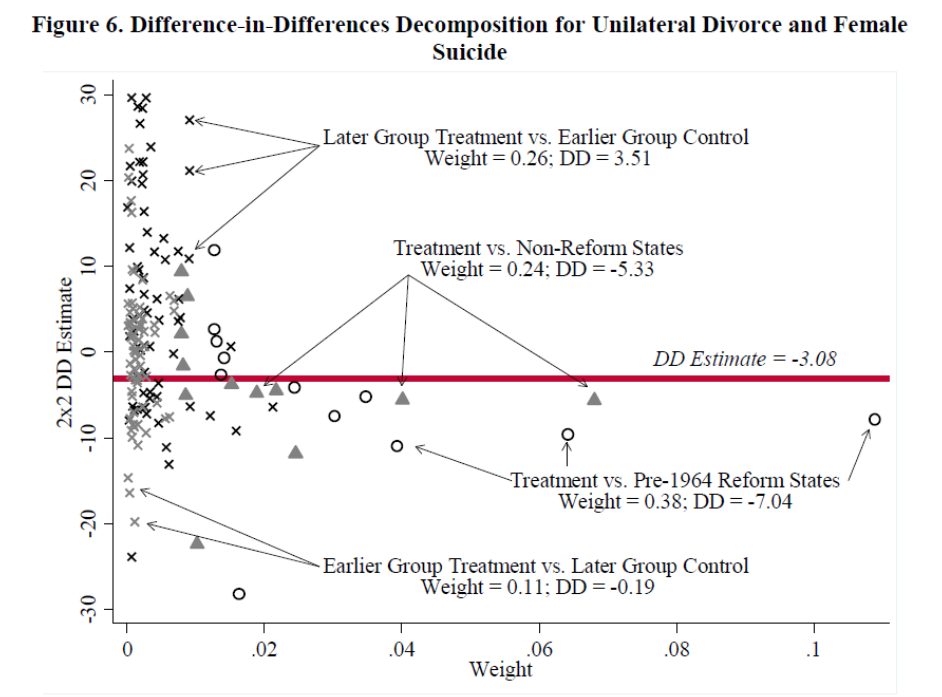
Diagnostic: the Bacon decomposition

  • The Bacon decomposition will take a TWFE model and decompose it into the full array of 2x2 d-i-d cells used to construct the overall estimate
  • The decomposition will also calculate the variance-weights used in regression to see which 2x2 cells are powering the overall estimate
castle_bacon <- bacon(l_homicide ~ post,
                      data = bacondecomp::castle,
                      id_var = "state",
                      time_var = "year") %>%
  arrange(treated, untreated)
                      type weight  avg_est
1 Earlier vs Later Treated 0.0598 -0.00554
2 Later vs Earlier Treated 0.0319  0.07032
3     Treated vs Untreated 0.9083  0.08796
treated untreated estimate weight type
2005 2006 -0.08313 0.003405 Earlier vs Later Treated
2005 2007 -0.11672 0.002095 Earlier vs Later Treated
2005 2008 -0.14123 0.001571 Earlier vs Later Treated
2005 2009 0.09714 0.001048 Earlier vs Later Treated
2005 99999 0.08017 0.045569 Treated vs Untreated
2006 2005 -0.14607 0.003405 Later vs Earlier Treated
2006 2007 0.08302 0.016342 Earlier vs Later Treated
2006 2008 -0.00848 0.016342 Earlier vs Later Treated
2006 2009 -0.08226 0.012256 Earlier vs Later Treated
2006 99999 0.06824 0.592395 Treated vs Untreated
2007 2005 -0.10806 0.001676 Later vs Earlier Treated
2007 2006 0.12596 0.010895 Later vs Earlier Treated
2007 2008 0.10372 0.002933 Earlier vs Later Treated
2007 2009 -0.01598 0.002933 Earlier vs Later Treated
2007 99999 0.11406 0.170124 Treated vs Untreated
2008 2005 -0.04898 0.000943 Later vs Earlier Treated
2008 2006 0.11069 0.008171 Later vs Earlier Treated
2008 2007 0.14479 0.001257 Later vs Earlier Treated
2008 2009 -0.17989 0.000838 Earlier vs Later Treated
2008 99999 0.14605 0.072910 Treated vs Untreated
2009 2005 0.17952 0.000419 Later vs Earlier Treated
2009 2006 0.11210 0.004085 Later vs Earlier Treated
2009 2007 0.00373 0.000838 Later vs Earlier Treated
2009 2008 -0.13078 0.000210 Later vs Earlier Treated
2009 99999 0.21108 0.027341 Treated vs Untreated
 
ggplot(castle_bacon) +
  aes(x = weight, y = estimate, shape = factor(type), color=factor(type)) +
  labs(x = "Weight", y = "Estimate", shape = "Type", color="Type") +
  geom_point() + 
  scale_color_viridis_d()

Adjustment: new estimators

R packages for new d-i-d estimators

Reference R package Description
Callaway Sant'Anna (2020) did Compare treatment only to never treated, or never-treated + not-yet-treated. Also propensity score weights with covariates.
Sun Abraham (2020) fixest NA
Chaisemartin D'Haultfoeuille (2020) DIDmultiplegt NA
Wooldridge (2021) fixest Dummies for all group, time, time-to-treat, time-since-treatment units
  • Background
  • Problem
  • Solutions
  • Case study - MISTI
  • Final thoughts

Measuring Impact of Stabilization Initiatives (MISTI)

Can small scale, community-driven development activities build local government legitimacy in a kinetic conflict-affected environment?

MISTI

  • Village panel survey in five waves, Sep 2012 - Nov 2014
  • ~5,000 villages surveyed across 130 districts and 23 provinces
  • ~ 30,000 household interviews per wave
  • 860 treated villages at any wave (17%)
  • 355 villages surveyed in all five waves
  • 85 villages treated (24%)

MISTI treatment timings

Wave Comparison villages Treated villages Treated villages (cumulative)
1 355 0 0
2 341 14 14
3 322 19 33
4 302 20 53
5 270 32 85

Single-wave analysis

  • Final reporting of MISTI relied on a series of single-wave estimations
Measure Wave 2-4 Wave 2-5 Wave 3-4 Wave 4-5 Wave 3-5
Stability 0.031 0.043 0.003 -0.039 -0.002
Government Capacity 0.044 0.054 0.032 -0.038 0.007
District Government Performance 0.053 0.053 0.046 -0.069 -0.031
District Government Satisfaction 0.006 -0.019 0.007 0.027 0.002
Provincial Government Performance 0.067 0.067 0.056 -0.064 0.005
Local Governance 0.012 0.031 0.031 -0.035 0.003
DDA-CDC Performance 0.000 0.035 0.034 -0.064 -0.015
Local Leader Performance 0.001 0.015 -0.001 0.045 0.015
Quality of Life 0.039 0.016 -0.003 -0.012 -0.027
Resilience 0.015 0.007 0.056 -0.004 0.017
Community Cohesion -0.029 -0.014 -0.044 0.027 0.058
Social Capital -0.037 -0.022 -0.095 0.001 0.074
Local Leader Satisfaction 0.009 0.016 0.022 0.046 0.028

MISTI TWFE

twfe <- lm(stab_std ~ treat_event + as.factor(village) + as.factor(wave),
           data=mistifull) %>%
  tidy()

twfe[1:2,]
termestimatestd.errorstatisticp.value
(Intercept)-0.05810.359 -0.1620.871
treat_event-0.03890.0947-0.4110.681

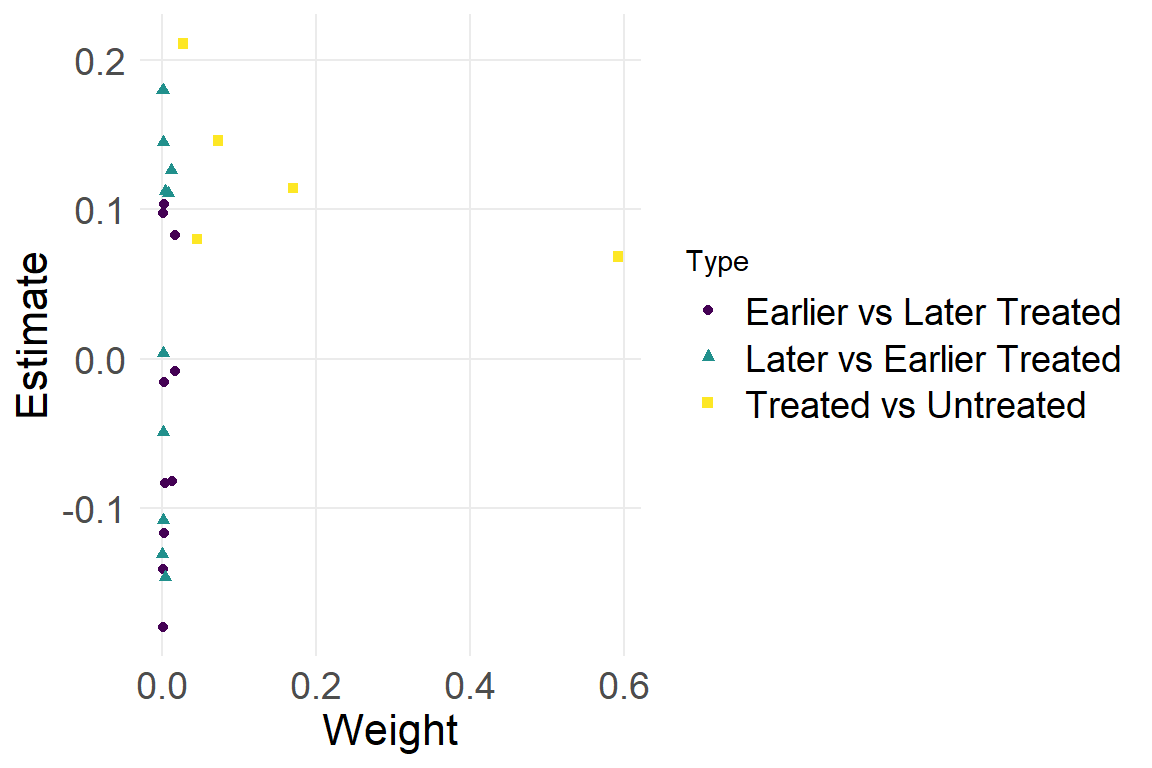
MISTI bacondecomp

mistibacon <- bacon(stab_std ~ treat_event,
                    data=mistifull,
                    id_var="village",
                    time_var="wave") %>%
  arrange(treated, untreated)
                      type weight avg_est
1 Earlier vs Later Treated 0.0578  0.3911
2 Later vs Earlier Treated 0.0466 -0.3465
3     Treated vs Untreated 0.8956 -0.0506
mistibacon_coef <- sum(mistibacon$estimate * mistibacon$weight)
mistibacon_coef 
[1] -0.0389
treated untreated estimate weight type
2 3 0.7473 0.00211 Earlier vs Later Treated
2 4 0.7093 0.00444 Earlier vs Later Treated
2 5 0.6868 0.01066 Earlier vs Later Treated
2 99999 0.8232 0.11998 Treated vs Untreated
3 2 -0.1216 0.00633 Later vs Earlier Treated
3 4 0.4973 0.00603 Earlier vs Later Treated
3 5 0.2976 0.01930 Earlier vs Later Treated
3 99999 0.1964 0.24425 Treated vs Untreated
4 2 -0.2707 0.00889 Later vs Earlier Treated
4 3 0.2135 0.00603 Later vs Earlier Treated
4 5 0.1182 0.01524 Earlier vs Later Treated
4 99999 -0.0291 0.25710 Treated vs Untreated
5 2 -0.5680 0.01066 Later vs Earlier Treated
5 3 -0.5686 0.00965 Later vs Earlier Treated
5 4 -0.5375 0.00508 Later vs Earlier Treated
5 99999 -0.6729 0.27424 Treated vs Untreated

Callaway and Sant’Anna (2020)

This estimation gives you multiple outcomes

  • Treatment by treatment group
  • An overall treatment effect
  • Overall dynamic effects / event study
  • Treatment effects by calendar time

Callaway and Sant’Anna replication

cal <- att_gt(yname="stab_std",
             tname="wave",
             idname="idname",
             gname="first.treat",
             xformla= ~ nsp + ln_dist,
             data=mistifull)
summary(cal)

Call:
att_gt(yname = "stab_std", tname = "wave", idname = "idname", 
    gname = "first.treat", xformla = ~nsp + ln_dist, data = mistifull)

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 

Group-Time Average Treatment Effects:
 Group Time ATT(g,t) Std. Error [95% Simult.  Conf. Band]  
     2    2   0.4105      0.381       -0.6179       1.439  
     2    3   0.9595      0.432       -0.2089       2.128  
     2    4   1.2952      0.452        0.0734       2.517 *
     2    5   0.5136      0.460       -0.7298       1.757  
     3    2  -0.2553      0.265       -0.9704       0.460  
     3    3   0.3693      0.258       -0.3271       1.066  
     3    4   0.3161      0.263       -0.3949       1.027  
     3    5   0.2650      0.220       -0.3305       0.861  
     4    2   0.1522      0.224       -0.4532       0.758  
     4    3  -0.3197      0.263       -1.0308       0.391  
     4    4   0.1823      0.274       -0.5590       0.923  
     4    5   0.0491      0.259       -0.6500       0.748  
     5    2   0.3244      0.203       -0.2243       0.873  
     5    3  -0.1808      0.191       -0.6978       0.336  
     5    4  -0.1153      0.170       -0.5752       0.344  
     5    5  -0.5982      0.181       -1.0881      -0.108 *
---
Signif. codes: `*' confidence band does not cover 0

P-value for pre-test of parallel trends assumption:  0.46101
Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Doubly Robust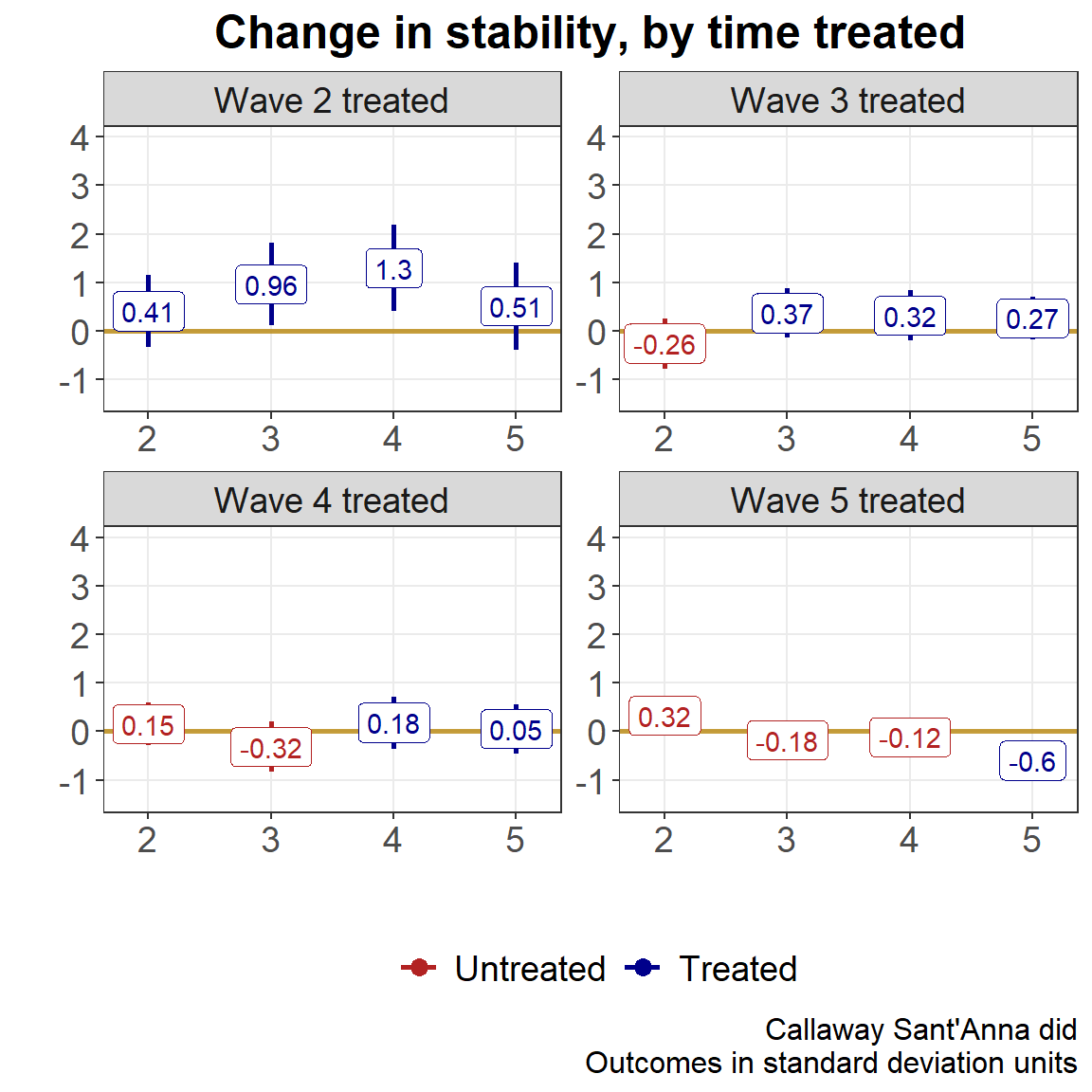
cal_simple <- aggte(cal, type="simple")
cal_simple

Call:
aggte(MP = cal, type = "simple")

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 


  ATT    Std. Error     [ 95%  Conf. Int.] 
 0.26          0.16    -0.0538       0.573 


---
Signif. codes: `*' confidence band does not cover 0

Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Doubly Robust
cal_dyn <- aggte(cal, type="dynamic")
cal_dyn

Call:
aggte(MP = cal, type = "dynamic")

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 


Overall summary of ATT's based on event-study/dynamic aggregation:  
   ATT    Std. Error     [ 95%  Conf. Int.]  
 0.392         0.191     0.0172       0.767 *


Dynamic Effects:
 Event time Estimate Std. Error [95% Simult.  Conf. Band]  
         -3   0.3244      0.214       -0.2291       0.878  
         -2  -0.0527      0.136       -0.4048       0.299  
         -1  -0.2104      0.123       -0.5282       0.107  
          0  -0.0322      0.135       -0.3815       0.317  
          1   0.3853      0.176       -0.0698       0.840  
          2   0.7021      0.241        0.0771       1.327 *
          3   0.5136      0.488       -0.7498       1.777  
---
Signif. codes: `*' confidence band does not cover 0

Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Doubly Robust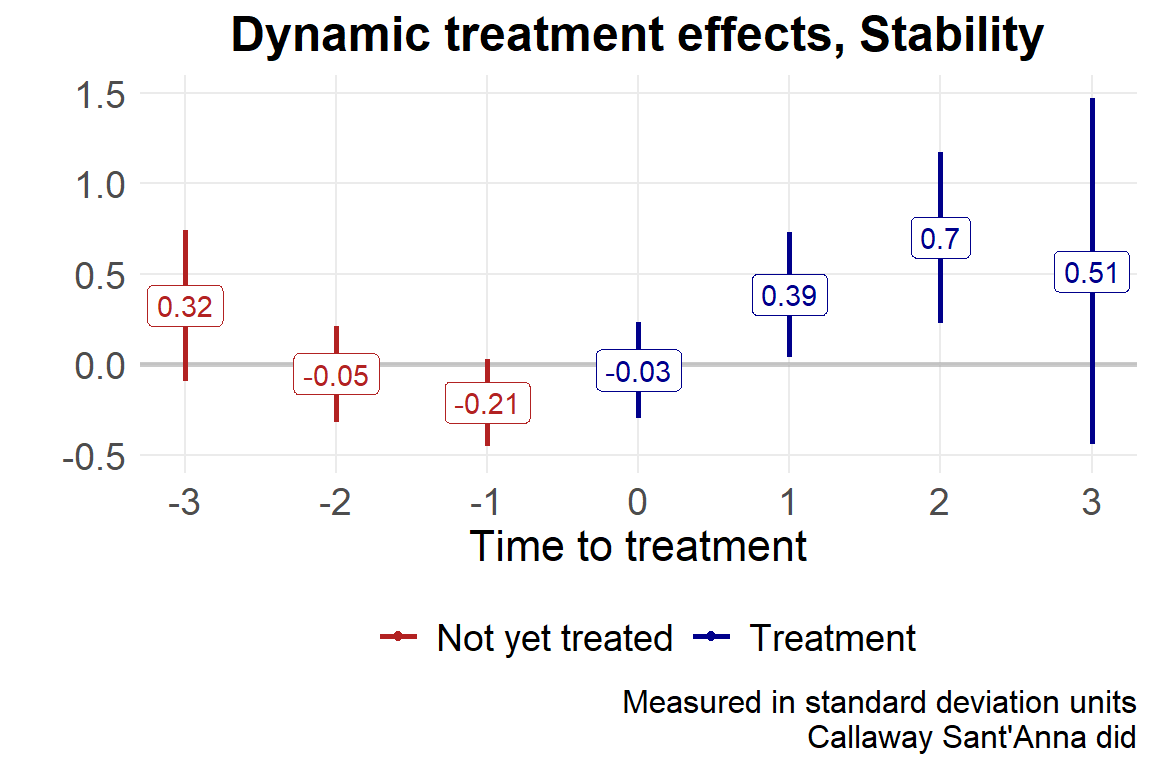
cal_grp <- aggte(cal, type="group")
cal_grp

Call:
aggte(MP = cal, type = "group")

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 


Overall summary of ATT's based on group/cohort aggregation:  
    ATT    Std. Error     [ 95%  Conf. Int.] 
 0.0037         0.116     -0.224       0.232 


Group Effects:
 Group Estimate Std. Error [95% Simult.  Conf. Band]  
     2    0.795      0.374       -0.0975       1.687  
     3    0.317      0.200       -0.1587       0.792  
     4    0.116      0.240       -0.4554       0.687  
     5   -0.598      0.181       -1.0305      -0.166 *
---
Signif. codes: `*' confidence band does not cover 0

Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Doubly Robust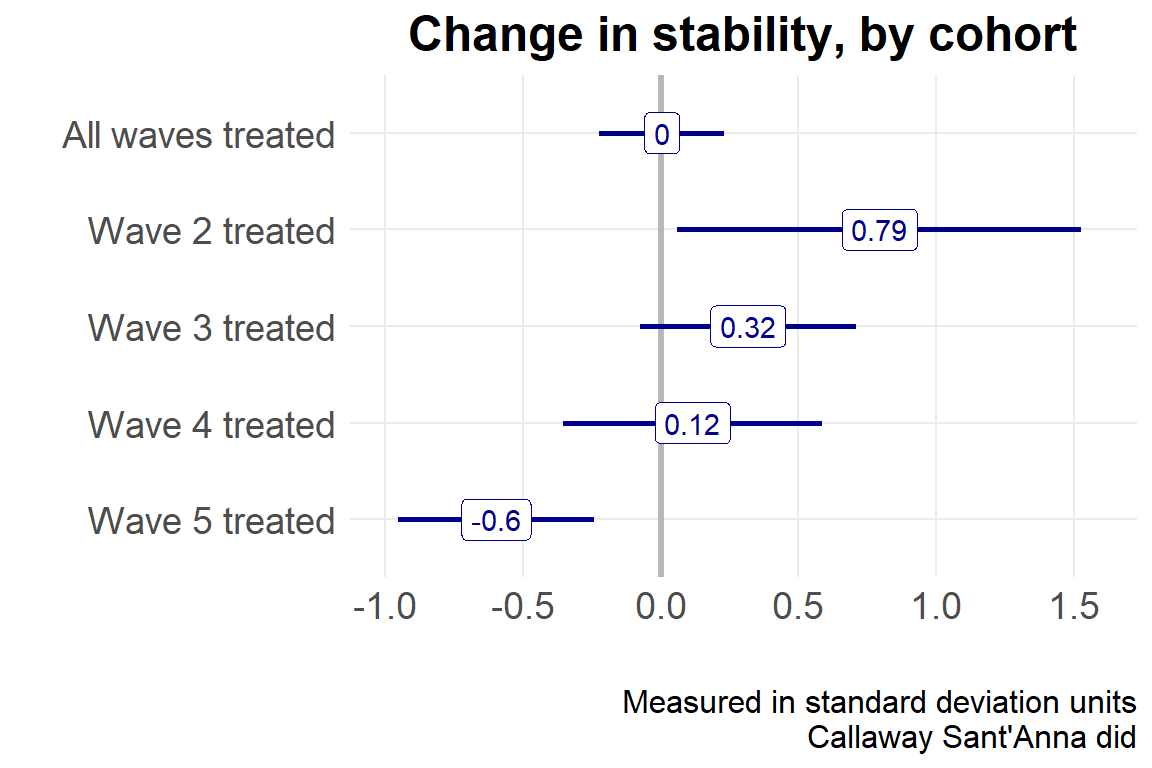
cal_cal <- aggte(cal, type="calendar")
cal_cal

Call:
aggte(MP = cal, type = "calendar")

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 


Overall summary of ATT's based on calendar time aggregation:  
   ATT    Std. Error     [ 95%  Conf. Int.]  
 0.371         0.179     0.0196       0.723 *


Time Effects:
 Time Estimate Std. Error [95% Simult.  Conf. Band]  
    2   0.4105      0.389       -0.5214       1.342  
    3   0.6197      0.245        0.0325       1.207 *
    4   0.5242      0.201        0.0432       1.005 *
    5  -0.0698      0.148       -0.4248       0.285  
---
Signif. codes: `*' confidence band does not cover 0

Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Doubly Robust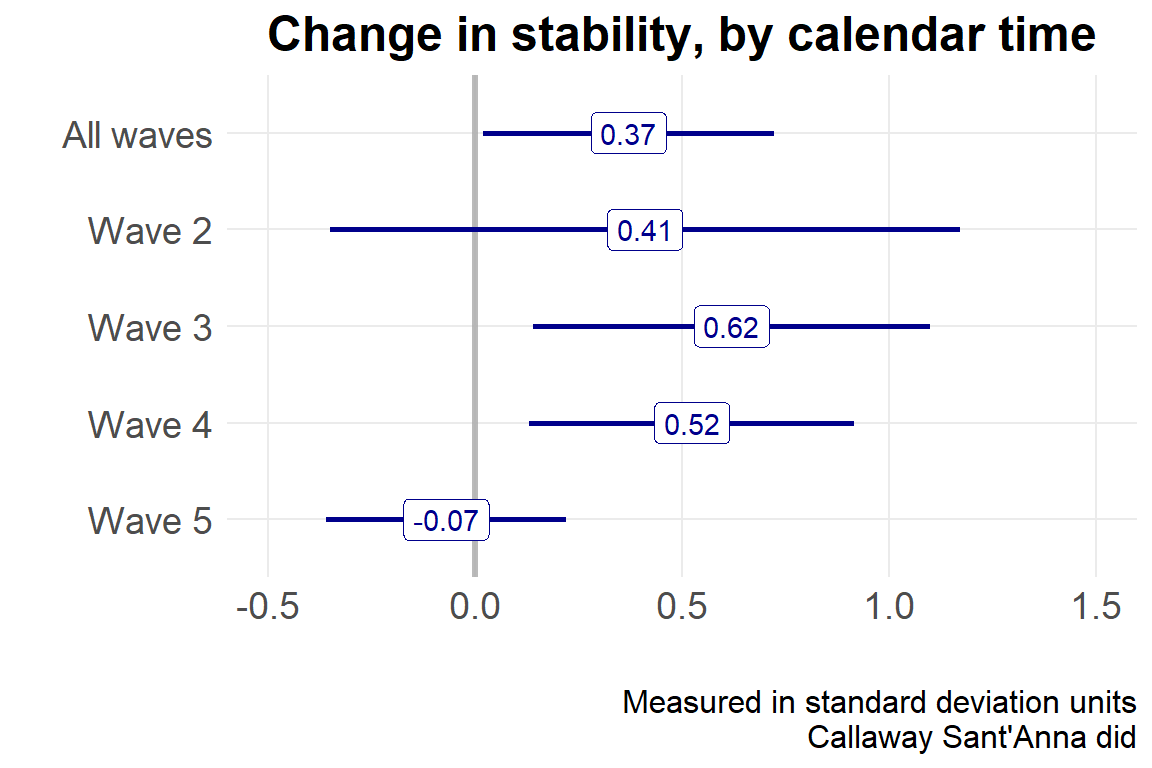
  • Background
  • Problem
  • Solutions
  • Case study - MISTI
  • Final thoughts

What have we learned?

  • In certain settings, two-way fixed effects estimation is biased in ways that we only recently came to realize
  • We have to carefully think through the data generating process (logic modeling) for each individual setting
  • As we get more granular data and ask deeper questions, econometric tools are starting to provide better insight into treatment dynamics

What should we do?

  • For any two-way fixed effects setting, use the Bacon decomposition to diagnose any problems
  • Use stacked d-i-d to remove problematic 2x2 cells, or apply any of the new estimators
  • Go back to your old evaluations!!

THANK YOU!!

dkillian@msi-inc.com

Please evaluate this session!

The next slide shows two DALL-E narratives

How would you rate the quality of this session, where 1 reflects the scenario on the left, and 5 reflects the scenario on the right?